機械学習を用いた一般物体検知のアルゴリズムに、SSD(Single Shot Multibox Detector)というものがあります。
深層学習の技術を使い、高スピードで多種類の物体を検知できます。
特定の物体を覚えさせ、その特定の物体を検知させることもできます。
このブログは、2編あるSSDについてのブログの第1編となっており、このアルゴリズムの理論を説明します。
本記事の目的は、初心者でもわかるような難易度にSSDのアルゴリズム理論を噛み砕いて説明することで、新しく機械学習・物体検知の世界に入りたい、コーディングはできないがとりあえず理論を理解したい、と考えている方々の助けになる事です。
より簡潔にハイレベルな内容がまとめられているのは、原著であるSSDの論文ですので、より詳しくはそちらをぜひ参照してみてください。
SSD: Single Shot MultiBox Detector
TensorFlowとKerasを用いたpythonの実装については、Avintonアカデミー受講者にコンテンツを提供予定です。Avintonではインターン、機械学習エンジニアを募集しています。
ご興味のある方は是非お問い合わせください。
また、物体検知をビジネスに生かしたい、というお客様へのAIシステム導入コンサルティングも実施しております。ぜひお気軽にご相談ください。
デフォルトボックスとは
SSDの肝となるのは、「デフォルトボックス(default boxes)」という長方形の「枠」です。
一枚の画像をSSDに読ませ、その中のどこに何があるのか予測させるとき、SSDは画像上に大きさや形の異なるデフォルトボックスを8732個乗せ、その枠ごとに予測値を計算します。

図1:8732個のデフォルトボックスを描画
8732個の枠を描画すると、画像が枠で埋め尽くされます。分解してみていくと、

図2:8732個のデフォルトボックスのうち、数十個をランダムに描画
このように様々な大きさの枠が様々な位置に描画されている事がわかります。
このデフォルトボックスの役割は、それぞれが、
1. 自身が物体からどのくらい離れていて、どのくらい大きさが異なるのか
2. そこには何があるのか
の2つを予測する事です。
これらを位置の予測とクラスの予測と呼びます。
具体的な例を見てみます。
先ほどの画像は、縦横が300\times300の大きさで、物体「車」が写っています。この画像に、デフォルトボックスを描画してみます。描画の便宜上、4つだけ選びます。

図3:緑が正解の座標、赤がデフォルトボックス(4つのみ選んで描画)
中心(center)の座標をcxとcy、幅(width)と高さ(height)をw,hとすると、物体とデフォルトボックスの座標はそれぞれ以下の表の通りです:
| id | cx | cy | w | h |
|---|---|---|---|---|
| 物体(車) | 207.5 | 162.5 | 140 | 200 |
| 1 | 208 | 176 | 134.0969 | 134.0969 |
| 2 | 176 | 176 | 156.9777 | 78.4888 |
| 3 | 56 | 72 | 34.6410 | 103.9230 |
| 4 | 204 | 144 | 111 | 111 |
表1:物体(車)と4つのデフォルトボックスの座標
位置の予測
上の例で、位置についてSSDが実際に出した予測値をみてみましょう。

図4:デフォルトボックスごとに差分符号化した予測先の座標
| id | \Delta cx | \Delta cy | \Delta w | \Delta h |
|---|---|---|---|---|
| 1 | 0.08 | −1.068 | 0.11 | −1.214 |
| 2 | 2.353 | −1.773 | −0.683 | 1.708 |
| 3 | 0.092 | 0.279 | 0.719 | −0.456 |
| 4 | 0.038 | 1.964 | 1.382 | -0.072 |
表2:4つのデフォルトボックスの出した位置の予測(差分符号化されている)
\Delta(デルタ)で表される座標は、対応するデフォルトボックスの座標を基準とした差分を表しており、このような表現形式を差分符号化(delta encoding)と言います。
この値はそれぞれ基準となるデフォルトボックスの座標などを使って変換することで、実際に予測した先の座標にすることができます。

図5:赤の実線が変換後の予測値(座標)、赤の点線が対応するデフォルトボックスの位置
| id | cx | cy | w | h |
|---|---|---|---|---|
| 1 | 209.07213 | 161.68217 | 137.08094 | 105.18074 |
| 2 | 212.93426 | 162.08465 | 136.94126 | 110.44376 |
| 3 | 56.31937 | 74.89882 | 39.99739 | 94.87071 |
| 4 | 208.42104 | 165.80191 | 146.33688 | 109.40799 |
表3:変換後の座標
車に被っていたデフォルトボックスが、全て車の位置に「寄って」行っていることがわかります。
この変換の計算について詳しくは第2篇で取り扱います。
クラスの予測
クラスの予測は、その枠が囲っているのがどの物体である可能性が高いかが、予測するクラスごとに確率で表現されます。

図6:クラス名と、そのクラスに属する予測(確率)
| id | background | car | boat | person |
|---|---|---|---|---|
| 1 | 0.0% | 99.916% | 0.001% | 0.0% |
| 2 | 100.0% | 3.772% | 0.008% | 0.0% |
| 3 | 100.0% | 0.04% | 0.221% | 0.202% |
| 4 | 0.0% | 96.67% | 0.013% | 0.0% |
表4:4つのデフォルトボックスの出したクラスの予測
ここでは、背景(background)の他に、ボート(boat)、車(car)、そして人(person)のどのクラスの物体であるかをそれぞれのデフォルトボックスが予測しています。
1と4のデフォルトボックスが、車であるとする高い予測値を出しました。
デフォルトボックスの選択
1も4も高い確率で車と予測しました。ここでもし「背景以外で8割以上の予測をした枠のみ残す」といったルールのみで枠を選ぶと、枠が重なり合って残ってしまいます。

図7:「背景以外で8割以上の予測をした枠のみ残す」ルールで予測先の枠を描画
ここでは、
- もっとも高い予測値を出した枠をまず選び、
- その枠に重なっている部分の面積(Intersection)が、枠を組み合わせた面積(Union)の5割以上の枠を全て消す
という操作をします。
この重なり度合いの指標をIntersection over Union(IoU)と呼び、上の操作のことをNon-maximum suppressionと呼びます。
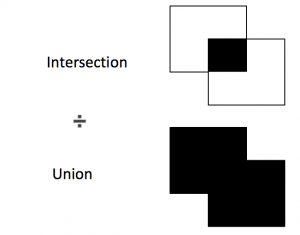
図8:Intersection over Union(IoU)
1と4の枠のIoUは5割を越しているので、予測値の高かった1のみ残し、4は消すことで、最終出力が得られます。

図9:Non-maximum suppression後の最終出力
このように、比較的高精度で、物体に枠をつける事ができました。
これでSSDの推論の説明は大まかに終わりです。とてもざっくりした説明ですが、流れは理解できたでしょうか。
おわりに
今回の記事では、主にSSDの推論について触れました。
次の記事では、主にSSDはどのように物体を学習するのかについて見ていきます。また、今回は触れなかった数学的側面にも触れます。
実際に学習が一回りする過程を丁寧に見ていきます。高校数学+α程度で理解できる範囲ですので、数学が苦手という方もぜひ読んでみてください。
また、更に進んで実際に物体の検知ができるコードを書きたい、もしくは物体検知をビジネスに活用したい、という方はぜひお問い合わせください。
合わせて読みたい関連記事
【機械学習入門】クラスタリング
【機械学習入門】教師あり学習と教師なし学習
【機械学習入門】機械学習に向けてのデータ前処理
Avintonアカデミー
あなたも、Avintonでこのような最先端技術を習得し活用してみませんか?
社員の成長を導きながら、AIやビッグデータなどの最先端技術をプロジェクトに活用していくことが私たちのビジョンです。Avintonの充実した技術研修でスキルアップを図り、あなたのキャリア目標を一緒に達成しませんか?









