Avintonでは、週末を有効活用しスキルアップのために勉強する会、ARoP(Avinton Road of Profesional) を定期的に開催しています。
毎回違うエンジニアたちが、それぞれの得意分野について知識をみんなに共有しています。
今回はプロジェクトでデータ解析を担当している、Iさんより社内勉強会で発表された内容を共有させていただきます。データ分析は社内エンジニアの中でも興味レベルの高い分野です。
初心者～ある程度経験のある方まで参考になる内容となっておりますので、
ご興味のある方、ぜひ読み進めてみてください。
EDA（探索的データ解析）とは
主にデータ分析初期に『データを理解するため』に行う作業で
モデリング等をする前の準備的な意味合いが強いものです。
データの分布や性質を確認すると共に、「数値か文字列か」や
「欠損値や異常値」の確認などの前処理的な作業も含まれています。
EDAのデキによってその後の作業効率が変わる重要な作業です。
さっそくEDAをやってみよう
◆今回使用するデータ
ポケモン最新作『ソード・シールド』に登場する408匹のポケモンの能力値とタイプを表すデータ。
データの読み込み
|
1 2 3 4 |
import pandas as pd url = 'https://raw.githubusercontent.com/thr3a/pokemon-stats/master/pokemon.csv' df = pd.read_csv(url, index_col=0) df.head() |
◆各カラムの説明
H～sumは能力を表しています。
h ⇒ HP
a ⇒ 攻撃
b ⇒ 防御
c ⇒ 特攻
d ⇒ 特防
s ⇒ 素早さ
sum ⇒ h～sの合計値（種族値）
【豆知識】
今回のデータは、indexにポケモンの名前が埋め込まれています。
df = pd.read_csv(url, index_col=0)
この「index_col」オプションでindexとして使用するカラムを列番号で指定しています。
試しにオプション無しでreadするとindexに番号が振られることがわかります。
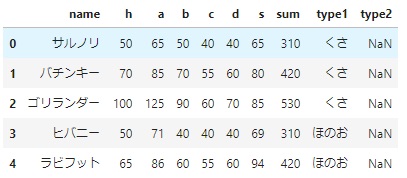
このindexの埋め込みの何が良いかというとデータの抽出がより直感的な操作で
できるようになります。
◆ピカチュウの攻撃力が知りたい時
[index埋め込みをしない場合]
「name」列が’ピカチュウ’の行を抽出して、その「a」列を参照します。
|
1 |
df[df['name'] == 'ピカチュウ']['a'] |
[index埋め込みをする場合]
行が’ピカチュウ’で、列が’a’のセルを参照します。
|
1 |
df.loc['ピカチュウ', 'a'] |
DataFrameには指定した行・列を参照するための「iloc・loc」属性があるので、
データを特定できる主キーとなる情報は、indexにした方が使いやすいことが多いです。
（ex.userID、時系列データの時間、シリアル番号など）
基本統計量の確認
|
1 |
df.describe() |
「type」の情報は文字列データなので結果から省略されています。
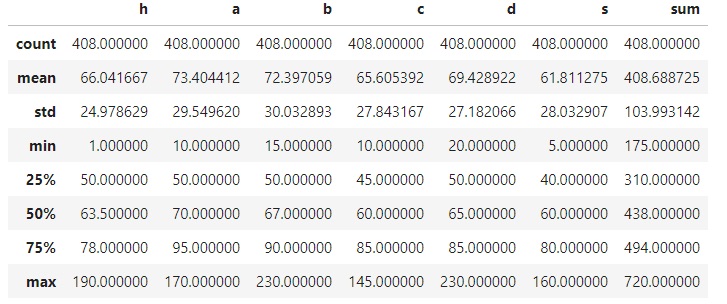
DataFrameを渡すと平均(mean)や標準偏差(std)等を一発で確認できて、
「type」の情報は文字列データなので結果から省略されています。
min～maxの値でデータにどういう偏りがあるか、分散しているかを確認できます。
標準偏差について
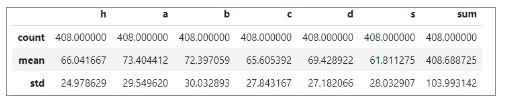
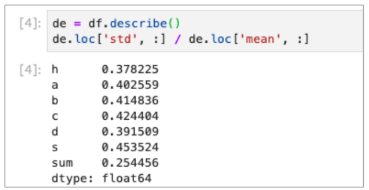
sumの標準偏差が大きい = ばらつきが大きい
のように見えるが、標準偏差は値のスケールの影響を受けるため
他の値と単純に比較できません。
単位や性質が異なる値の分散を相対比較する場合は、
「標準偏差/平均」で算出される「変動係数」を確認する必要があります。
|
1 2 |
de = df.describe( ) de.loc['std' , :] / de.loc['mean', :] |
|
1 2 3 4 5 6 7 8 |
h 0.378225 a 0.402559 b 0.414836 c 0.424404 d 0.391509 s 0.453524 sum 0.254456 dtype: float64 |
今回のデータで変動係数を計算すると、むしろsumのばらつきが最も小さいことがわかります。
groupbyを使った基本統計量
|
1 2 |
df_type1 = df.groupby(['type1']) df_type1.describe() |
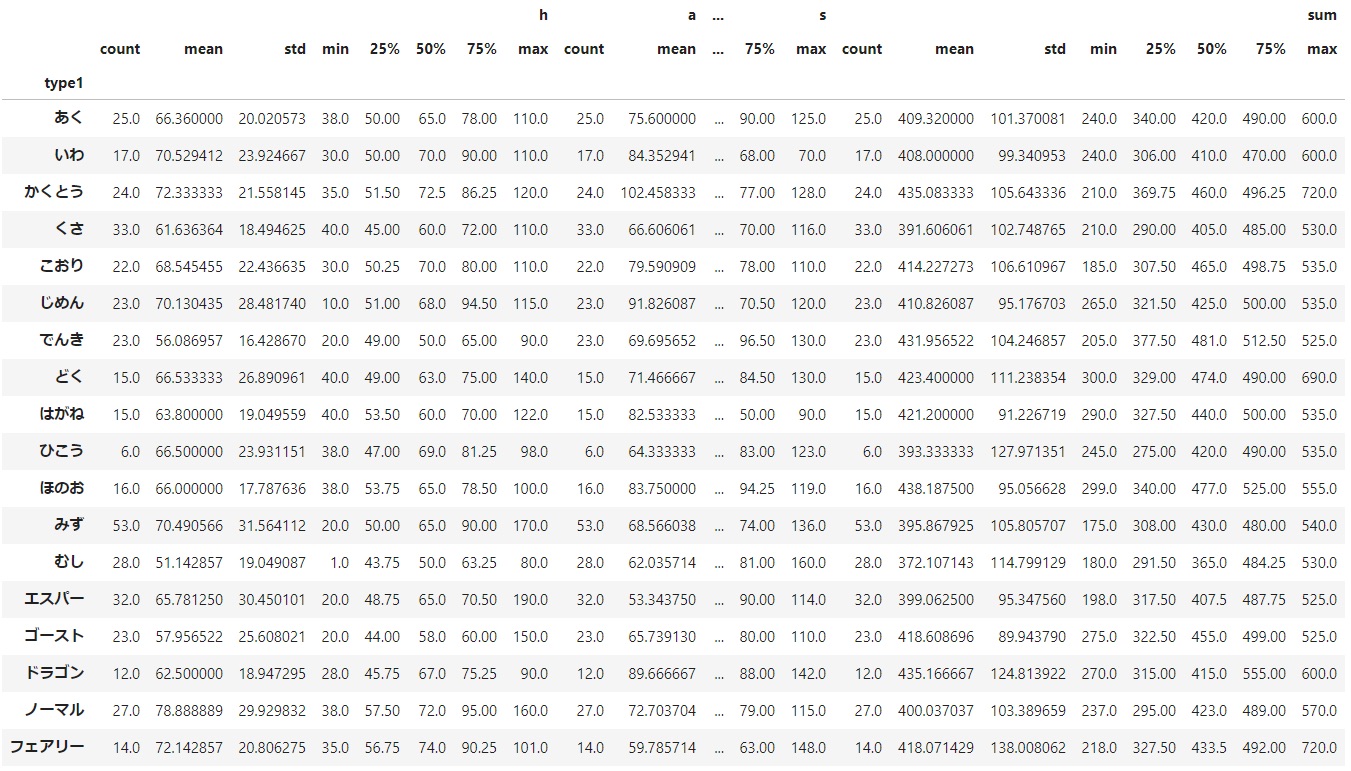
特定のカラムに着目して基本統計量を作成することも可能。
欠損値の確認
|
1 |
df.isnull().any() |
今回はtype2に欠損値あることは正常なのでそのままにしますが、
期待しない欠損がある場合何らかの値（平均や中央値）で埋めるか、
そのデータを削除することでデータを成形していきます。
散布図行列
|
1 2 3 4 |
import matplotlib.pyplot as plt from pandas import plotting plotting.scatter_matrix(df.loc[:, 'h':'sum'], figsize=(10, 10)) plt.show() |
散布図をプロットすることで、データ同士の関係を視覚的に確認できます。
jupyter上で見てみましょう！
相関行列
|
1 2 3 |
import seaborn as sns cor = df.corr() sns.heatmap(cor, square=True, cmap='plasma', vmax=1,vmin=-1, annot=True) |
相関係数とは…
データ間にどれだけ強い関係性があるかを示す指標。
-1～1までの値を取り、絶対値が大きいほど相関が強いことを表します。
また、「Aが増える程Bが上がる」正の相関と
「Aが増えるほどBが下がる」負の相関が存在します。
相関係数が負の数の場合は、負の相関を表しています。
演習確認
ポケモンGOのデータ(csv)を使用して､同じようにデータを観察してみましょう｡
Data>Columnsに各カラムの説明があります｡
特にポケモンGOでは｢CP｣という値がポケモンの強さを表しているため
｢MaxCP｣がポケモンの強さを表しています｡
基本統計量の確認
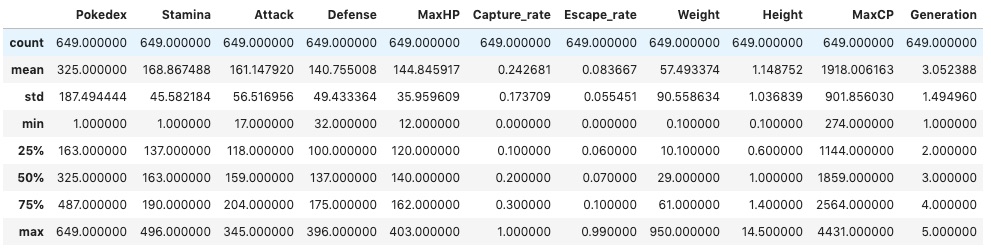能力値に関しては、中央値・平均値も揃っており特に特徴はなさそう。
MaxCPも中央値に対して平均値が誤差5%未満のため、
ある程度まとまっている印象です。
散布図行列
MaxCPとの関係性を見ていくと、明らかに「Attack」が線形の関係になっています。
MaxHP、Defenseもある程度は関係がありそうです。
相関行列
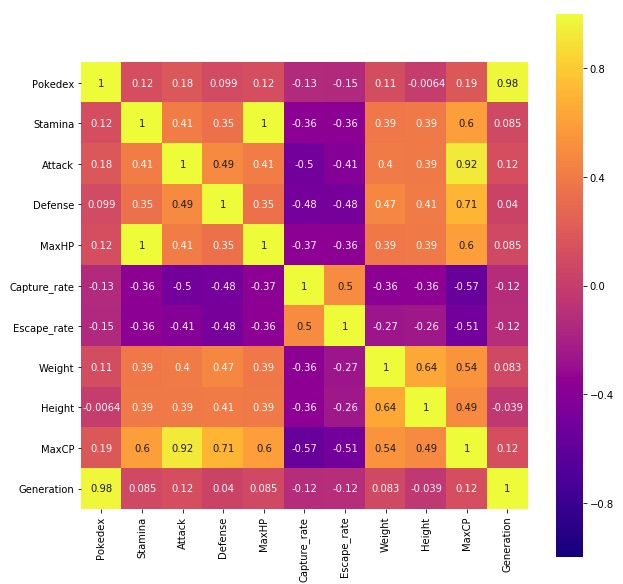
やはりMaxCPとAttackがずば抜けて相関が高くなっています。
「Attackが高いポケモンが強い」ということは言えそうです。
どういうポケモンが強いのだろう
多分、伝説ポケモンは強いんだろうなあ…
やはり強い…
MaxCPは特に平均・中央値が共に約2倍あり、更に標準偏差が半分しかないので
強いところに伝説ポケモンが密集していることがわかります。
どういうタイプのポケモンが強いのだろう
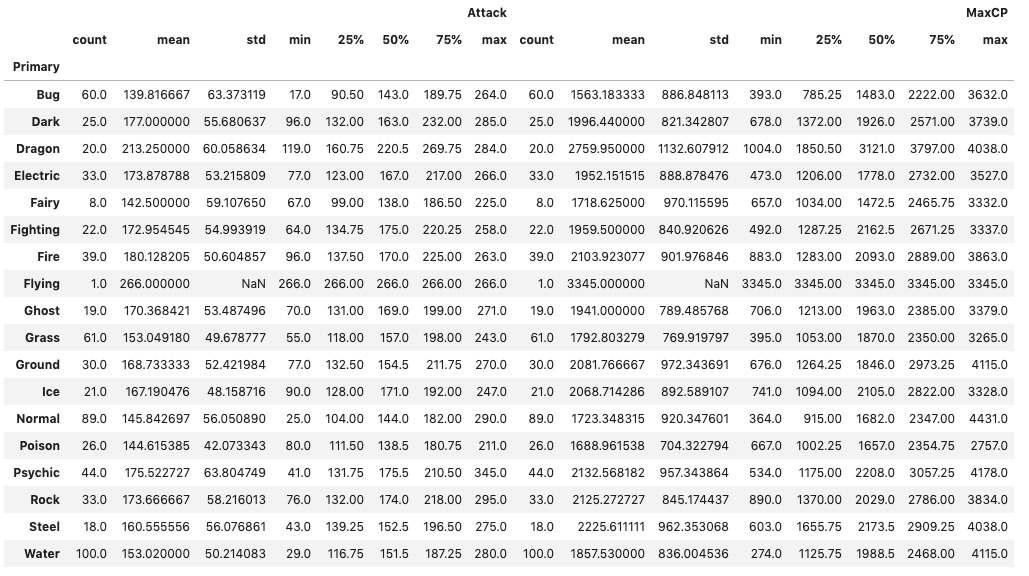Dragon typeのポケモンが抜けて強いことがわかります。
次点でDark,Psychicあたりでしょうか。
今度は、「伝説ポケモンが強い」「Dragonポケモンが強い」
ということをもう少し視覚的に確認してみます。
散布図行列（色分け）
|
1 |
plotting.scatter_matrix(de.iloc[:, 1:-1], figsize=(20, 20), c=(de['Legendary']=='No'), cmap='bwr') |
オプションの「c」でプロットを色分けすることができます。
（cmapはその配色を決める値）
cオプションに対して値を渡すとその値の種類の数だけ色分けをしてくれます。
青が伝説ポケモンの分布ですが、明らかにMaxCPが高いエリアに集中していることが一目瞭然でわかります。
|
1 |
plotting.scatter_matrix(de.iloc[:, 1:-1], figsize=(20, 20), c=(de['Primary']=='Dragon'), cmap='bwr') |
同様にDragonポケモンの確認
|
1 |
plotting.scatter_matrix(de.iloc[:, 1:-1], figsize=(20, 20), c=(de['Primary']=='Dragon'), cmap='bwr') |
参考までに比較的値が低かったBugポケモンと比較
他の着目点
「Capture_rate」と「MaxCP」に着目してもっとも「捕獲難易度に対してのコスパが
いいポケモン」を探すこともできます。
今回のデータであれば、黒線で囲んだ点が限りなく捕獲しやすい上にCPが高く
圧倒的コスパの良さを発揮しています。
しかし、これは伝説ポケモンであるため次にコスパが良いのは赤丸です。
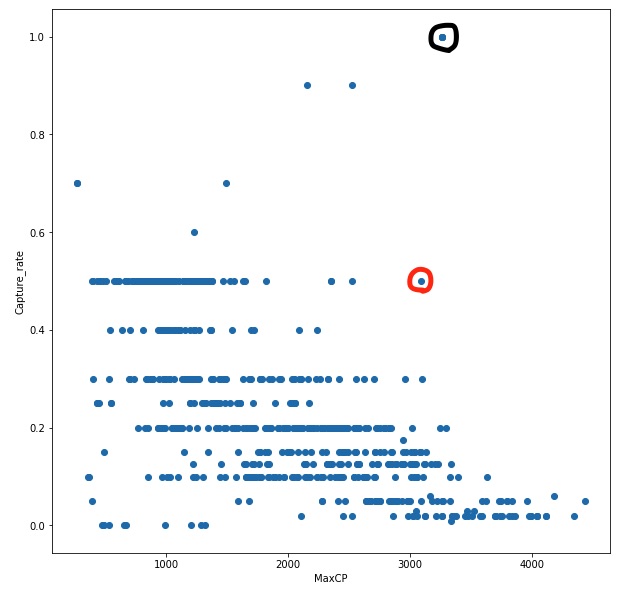
※ちなみにGallade（エルレイド）というポケモンでした。
特徴量エンジニアリングについて
今回のように、分析したい対象のデータに対して比較的に簡単に関連性の高いデータが見つかる場合もありますが、勿論見つからないケースも多々あります。
また、現状の分析結果や作成したモデルの精度を高めるために
生データには無いデータを作成したり、データを変換することがあります。
そういった操作のことを特徴量エンジニアリングと呼びます。
PCA（主成分分析）
※PCAはEDAとしてよく紹介されますが、便宜上こちらで紹介させてください
PCAとは次元削減法でよく使われる手法で、相関の高い多変数から新たな変数を
合成する手法です。
ただし合成された変数の意味は人間が意味づけする必要があります。
PCAは「教師なし学習」の一種とされていて、sklearnから以下のような流れで使うことができます。
|
1 2 3 4 5 6 7 8 9 10 11 |
from sklearn.decomposition import PCA pca = PCA() pca.fit(df.loc[:, 'h':'s']) feature = pca.transform(df.loc[:, 'h':'s']) plt.figure(figsize=(8, 8)) plt.scatter(feature[:, 0], feature[:, 1], alpha=0.8) plt.xlabel('PC1') plt.ylabel('PC2') plt.grid() plt.show() |
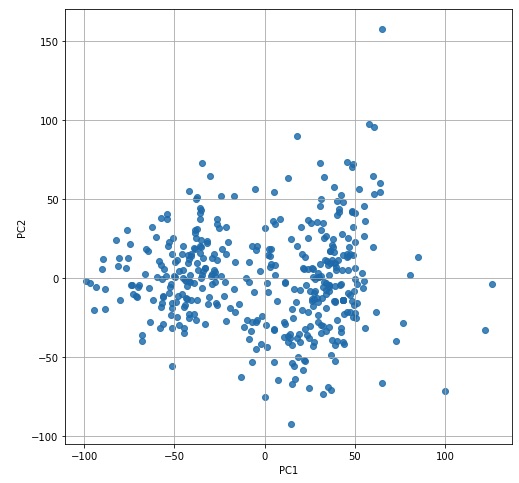
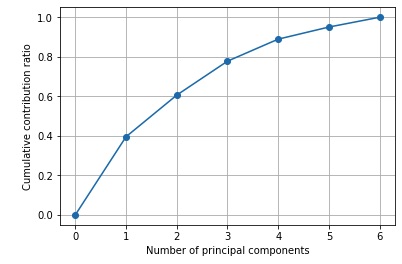
累積寄与率
PCAした際にあわせて確認しなければならないのが寄与率です。
寄与率は「その値がデータをどのくらい説明できているか」を表す数値です。
|
1 2 3 4 5 6 7 8 |
import matplotlib.ticker as ticker import numpy as np plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True)) plt.plot([0] + list( np.cumsum(pca.explained_variance_ratio_)), "-o") plt.xlabel("Number of principal components") plt.ylabel("Cumulative contribution ratio") plt.grid() plt.show() |
PCAで作成した特徴への意味づけ
PCAで特徴量を作成したら、今度はその特徴にどういう意味があるかを探っていきます。
まずはドラゴンポケモンのみを色を付けてプロットしてみる。
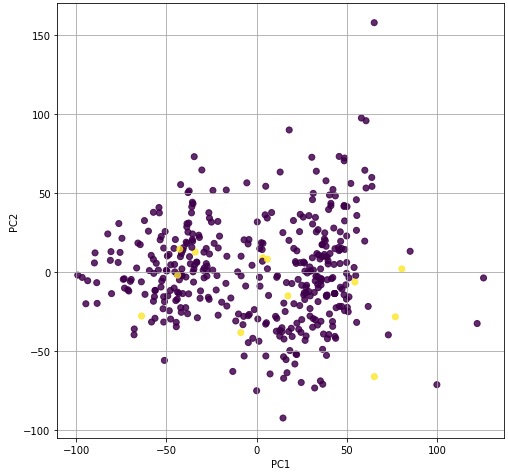ドラゴンポケモンであるかは関係がなさそうです。
結果的には、PC1が種族値（合計値）でPC2が素早さでほぼわかれていることがわかりました。
※今回は新しい特徴は生み出せていない…
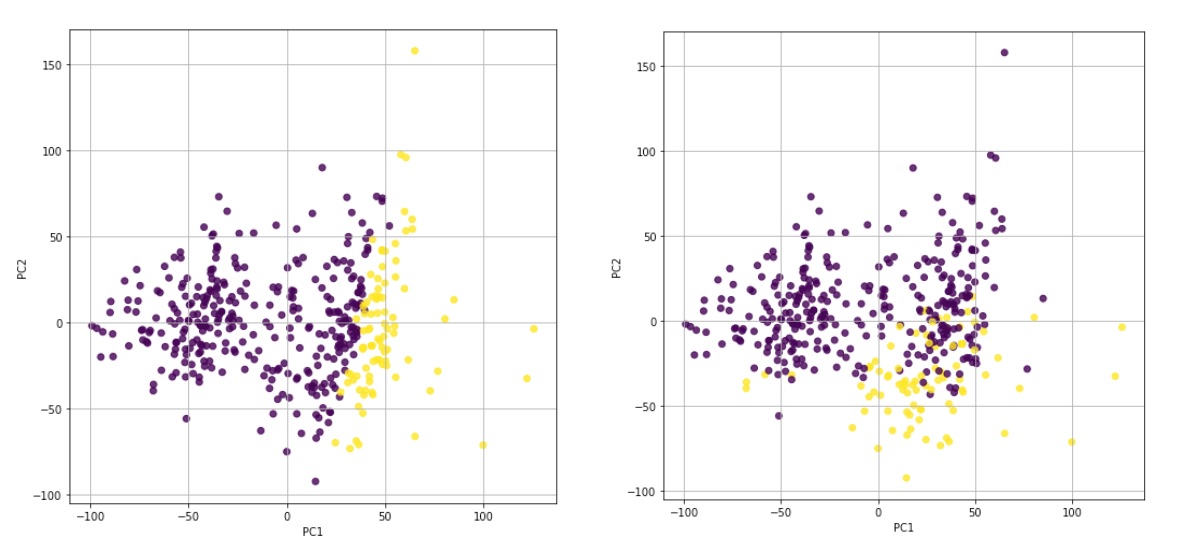
結果から読み取れること
今回のポケモンデータから、PCAで有効な特徴量を新たに得ることはできませんでした。
しかし、PCAで重要なことは累積寄与率からポケモンを説明するには「種族値」が最も重要で次に「素早さ」が重要であるということがわかったことです。
そして、その2つで約60%は説明できるという定量的な結果が得られることです。
ここから、予測モデル作成のためのデータ選定に活かす等の使い道があります。
ビニング
例えば身長のデータがあった時、値をそのまま使うのではなく
「150-155」のグループ「155-160」のグループ等、ある程度の範囲を持たせて
グループ分けする手法。
一見情報が欠落しているように見えるが、
明示的にデータを与えることでより結果がわかりやすくなる場合がある。
モデル作成においても同様に精度上昇する場合がある。
Target Encoding
目的変数を用いてカテゴリ変数を変換する手法。
機械学習モデルにカテゴリ変数をそのまま入れることはできないので
普通はOneHotEncodingをするのが最も一般的ですが、Kaggle等では
モデル精度を上げるための定石のような感じになっています。
基本的には、あるカテゴリ変数の値ごとに目的変数を集計し平均値を算出します。
その平均値をカテゴリ変数と置き換えて学習させるというものです。
トレンド（季節性）除去
時系列データにおいて、季節性により発生する傾向を除去し
より真のデータの動きを取得するための手法。
statsmodelsというライブラリを使うと、時系列データを
「トレンド成分」「季節成分」「残差」に分解することができます。
※一番上が生データで、下3つが分解結果
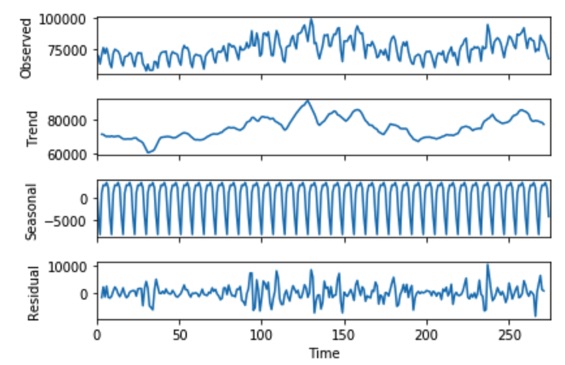例えば店舗の売り上げを分析する際、一般的には平日より休日の方が
売り上げが高くなります。
そのままでは、平日と休日を単純に比較ができないため「毎週土日に売り上げが上がる」という周期的な季節性を除去することで、より汎用的な分析が可能になります。
周期を年で見れば夏冬での違い等を吸収することができます。
まとめ
今回はEDAの手法とその後の特徴量エンジニアリングについて触れました。
今後、データ分析に興味ある方は是非試してみて下さい！
次回は、この勉強会に参加したエンジニアが参加者目線でレポートする予定です！
Avintonはエンジニアの教育に力を入れています。Avintonアカデミーで最新技術を学びませんか？
採用に関してはこちら。未経験エンジニアも積極採用しています！
