機械学習アルゴリスムの1つであるクラスタリングという手法について紹介します。
このクラスタリングは、既存のデータを元に予測や認識などのタスクを行うというよりも、データの構造を理解する際により多く用いられます。
クラスタリングの概要
動画:TensorBoard: Embedding Visualization
クラスタリングとは、類似度をもとにデータをグループ分けをする手法です。教師なし学習のひとつです。似た特徴をもとにデータグループを作り、それらをクラスタに分けていくのがこのアルゴリズムの目標です。
下図はデータが2次元と低次元のため、人の目で見ても2グループに分類されることが明らかですが、上の動画のように、高次元・多グループになると、人が判断することは困難です。
クラスタリングは、こうしたデータのグループ分けを、人力ではなくコンピュータによる処理で実現できます。
クラスタリングのタイプ
大まかに言うと、クラスタリングは2つのサブグループに分けることができます。
| タイプ | 内容 |
|---|---|
| ハードクラスタリング | ハードクラスタリングでは、それぞれのデータ点は1つのクラスタに完全に属しているか否かの二択です。例えば上の小売店の例では、それぞれの顧客は10グループのうちのどれかに必ず割り当てられます。 |
| ソフトクラスタリング | ソフトクラスタリングでは、それぞれのデータ点が別々のクラスタに1か0かで完全に割り当てられるのではなく、そのデータ点がそのクラスタたちに属する確率ないしは尤度が計算されます。例えば先ほどの例では、個々の客がそれぞれのクラスタに属する確率が計算されます。 |
クラスタリングアルゴリズムのタイプ
クラスタリングというタスクは自由度が大きいので、このタスクを達成するために用いられうる手段は山ほどあります。そしてその方法1つ1つがそれぞれ異なるルールに従ってデータ点間の”類似度”を定義しています。
実際、100以上のクラスタリングアルゴリズムが世の中には存在します。ただよく使われているのはその中のほんの一部です。それらよく使われるものを少し詳しく見ていきましょう。
| タイプ | 内容 | 主な例 |
|---|---|---|
| Connectivity models | 名前から予想できるように、これらのモデルはデータ空間中でより近いデータ点同士は、互いにより類似しているだろうとの考えに基づいています。このモデルには2つのアプローチがあります。
1つ目のアプローチでは、まず全てのデータ点を別々のクラスタに分類します。その上でそれらのデータ点の距離が短くなるようにデータ点をまとめていきます。 2つめのアプローチでは、全てのデータ点は1つのクラスタとして分類され、その中で距離が長くなるように分割されていきます。また距離関数の選択にも自由があります。 これらのモデルは、解釈はしやすいですが大きなデータセットの扱いに対しては拡張性に欠けます。 |
階層的クラスタリング |
| Centroid models | これらは反復クラスタリングアルゴリズムで、類似度はクラスタの重心とデータ点との距離から導かれます。
これらのモデルでは、最終的なクラスタ数を事前に指定しておく必要があり、データセットに対する事前知識を持っておく必要があります。そして反復処理によって局所最適解を見つけます。 |
K Means |
| Distribution models | このモデルは、1つのクラスタに属する全てのデータ点が、同じ確率分布(例えば正規分布やガウス分布)に従う見込みがどれほどあるかに基づいています。オーバーフィッティングに陥りやすいのが特徴です。 | 多変数正規分布を用いるEMアルゴリズム(期待値最大化法) |
| Density models | これらは、データ空間中でデータ点の密度の異なるエリアを探します。密度の異なるエリアを分離し、そのエリア内のデータ点を同じクラスタに割り当てます。 | DBSCAN、OPTICS |
K Means クラスタリング
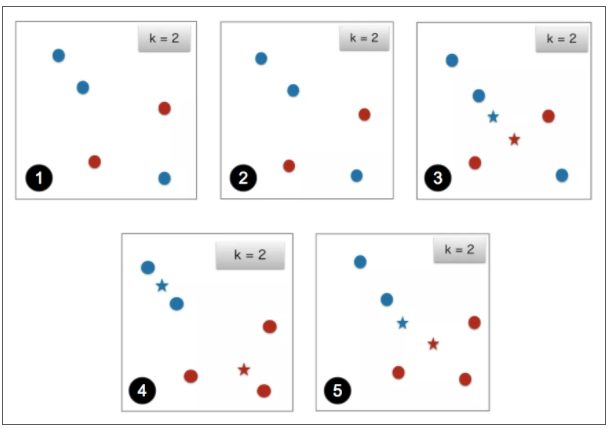
クラスタリングアルゴリズムの5つのステップ
K Means クラスタリングは、非階層型クラスタリングの手法で、1回の処理ごとに極大値を見つける反復クラスタリングアルゴリズムです。階層型クラスタリングとの大きな違いは、いくつのクラスタに分割するか、あらかじめ決める必要があるという点です。このアルゴリズムは以下の5ステップからなります。
- クラスタの数を指定する: ここでは22次元空間で以下の5つのデータ点を2つのクラスタに分けることを考えます。
- ランダムにそれぞれのデータ点をクラスタに割り当てる: この例では青色のデータ点をクラスタ1に、赤色のデータ点をクラスタ2に割り当てます。
- クラスタの重心を計算する: 例で、青色のクラスタのデータ点の重心は青色の★印で、赤色のクラスタのデータ点の重心は赤色の★印で表しています。
- それぞれのデータ点を一番近いクラスタ重心に割り当てしなおす: ここでは図で一番下のデータ点のみが、赤色のクラスタ重心により近いにもかかわらず青色のクラスタに割り当てられているのでこれを赤色のクラスタに割り当てなおします。
- 再度クラスタの重心を計算しなおす: ここでもう一度両クラスタの重心を計算しなおします。
- 更新がなくなるまでステップ4、5を繰り返す: 同様にして4番目のステップと5番目のステップを大域的最適解に達するまで繰り返します。2回繰り返してもデータ点のクラスタが切り替わらなければアルゴリズムの終了を意味します。もしそうでなければ明示的に指示されます。
なお、K meansクラスタリングは教師なし学習の一種ですが、教師信号・ラベルを自ら生成しながら学習を行うという意味で、教師あり学習の特別な場合だという解釈もあります。
階層型クラスタリング
階層型クラスタリングは、名前からもわかる通りクラスタの階層を組み上げていくアルゴリズムです。階層型クラスタリングには、ボトムアップ型とトップダウン型がありますが、今回はボトムアップ型をご説明します。
このアルゴリズムでは、まず全てのデータ点にそれぞれ1つずつクラスタを割り当てます。そして2つの最近接データ点を同じクラスタにマージします。最終的には、クラスタ数が1つになるまでマージしていきます。
データ同士の距離を比較し、近いデータ同士を結合させてボトムアップでまとめていくため、距離をどのように定義するかが重要です。
階層的クラスタリングの結果は、樹形図を用いて表すことができます。
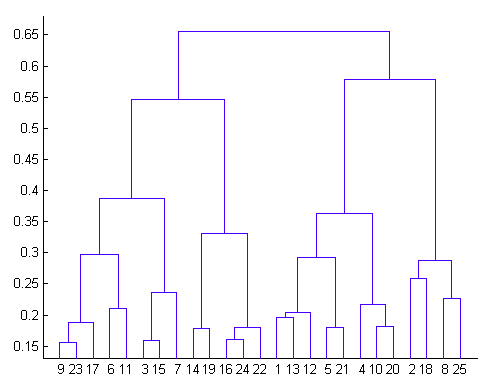
画像:An Introduction to Clustering and different methods of clustering
階層型クラスタリングの結果は、上のような樹形図(デンドログラム)を用いて表すことができます。
図の最下部、まずはそれぞれが別々のクラスタとして設定された25個のデータ点から始めます。そして最上部で1つのクラスタにまとめられるまで、最近接の2つのデータ点をマージしていきます。樹形図上で2つのクラスタがマージされる高さは、データ空間でのその2つの距離の大きさを表しています。
樹形図を詳しく見ることで、どのクラスタ数がそのデータ点群のグループ分けを最もよく表現するかを決めることができます。最良のクラスタ数は、垂直方向の距離が最大になるように水平方向に2本の直線をクラスタとぶつかることなく引いた時の、その間の垂直方向の線の数によって決まります。
上の例では、最良のクラスタ数は4ということになります。なぜなら下の樹形図中の赤の水平方向の2線が、垂直方向の最大距離ABをカバーしているからです。
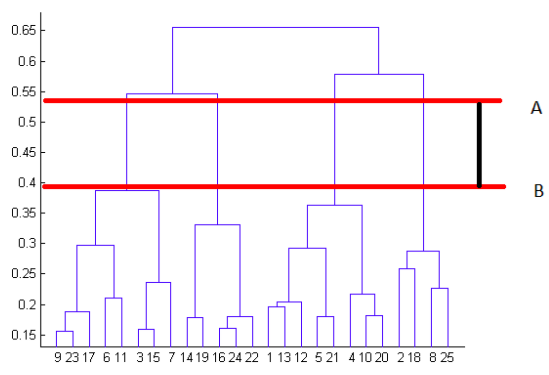
画像:An Introduction to Clustering and different methods of clustering
クラスタリングの応用
クラスタリングは幅広い範囲に数多くの応用先があります。最もよく見る応用先のいくつかの例として以下があげられます。
- レコメンドエンジン
- マーケットセグメンテーション
- ソーシャルネットワーク分析
- 検索結果のグループ分け
- 医療画像処理
- イメージセグメンテーション
- 異常検知
まとめ
ここまででクラスタリングアルゴリズムの概要と、代表的なアルゴリズムの詳細を説明してきました。なおクラスタリングはライブラリを使えば実装は簡単ですが、データ量やデータ中の外れ値などに結果がかなり依存してしまう点には注意が必要です。
今後も機械学習入門者の方々のために、技術ブログを定期的に公開し、機械学習の基本を網羅できるよう解説していきます。ぜひブログチェックしてください!
関連記事
【機械学習入門】教師あり学習と教師なし学習
【機械学習入門】 深層強化学習の基礎
未経験エンジニアのためのプログラミング学習コンテンツ Avintonアカデミー
機械学習を用いた画像分類体験
機械学習入門者向け ChainerRLでブロック崩しの学習
機械学習入門者向け ランダムフォレストによるTitanic生存者予測
Avintonが提供する6つの機械学習サービス事例









