
SVMは教師ありの機械学習アルゴリズムです。基本的には分類と回帰のどちらのタスクにも利用可能ですが、実際のところは分類タスクにより多く利用されています。
高速で信頼性のある分類アルゴリズムで、少ないデータ量でもよい性能が期待できます。Example code付きですので、ぜひ自分でも実際にアルゴリズムを動かしてみて、理解を深めてみてください。
SVMとは
簡単のため、特徴量が2つしかない2次元データのデータセットを考えます。するとSVMでは、対象のデータセットをクラスの応じて最も適切に分割する直線を見つける、というのが基本となる考え方になります(下図は2クラス分類の場合)。
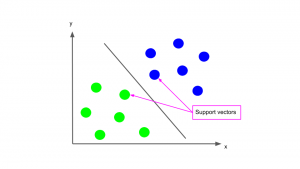
Support vector
アルゴリズムの名前にも出てくるSupport Vectorとは、そのデータセットを分割する直線に最も近いデータ点のことを指します。SVMでは、このSupport Vectorがそのデータセットを分割する直線を決める際に大きな役割を果たします。詳しくは次のセクションで説明します。
この分割直線が決まれば、後は判別したいデータがこの直線のどちら側の領域にあるかでクラスの判別を行います。上のグラフで言えば、直線の左にデータがあればそれは黄緑のクラス、右にあれば青のクラス、ということになります。
SVMの仕組み
単純な例を用いて説明します。x, y2つの特徴量をもとに、データが青と黄緑のどちらのクラスかを分類する分類器をつくりたいとします。まずはx-y平面上に、すでにクラス分けされたトレーニングデータを考えます。
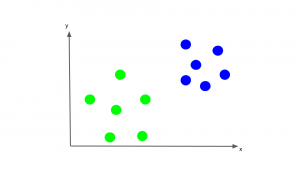
先ほども述べたように、SVMでは、このトレーニングデータを、各データのクラスも考慮して1番適切に分離するような直線を見つけ出します。そしてこの直線を境に、一方のサイドに位置するデータを全て青、もう一方のサイドに位置するデータを全て黄緑と分類します。このことから、この直線のことを決定境界と呼ぶこともあります。
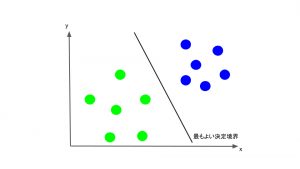
ではその”最も適切に分離する直線”は具体的にどのように決められるのでしょうか。SVMでは、それぞれのクラスで、その直線に最も近いデータ点(Support Vector)を考え、そのデータ点と直線との距離(マージン)が、できるだけ大きくなるように直線を決定します。
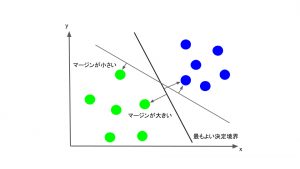
以上がSVMでの決定境界の決め方になります。
応用例
SVMはそのアルゴリズムの仕組みからも、主に分類タスクに用いられます。
テキスト分類

文章をあらかじめ用意したカテゴリに分類することができます。
具体的には、スパムメールの検出に用いられています。
なお、文章を機械学習アルゴリズムで扱うときは、基本は文章を単語ごとなどに分割し、それぞれに数字を割り当て数データに変換してから扱います。
数字認識

手書きの数字の画像のピクセル値をデータに、それを0~9などの数字カテゴリに分類することもできます。
郵便番号の認識などが具体的な利用例です。
顔検出

数字認識と同様、画像のピクセルの値から、その画像に顔が含まれているか否か、含まれていれば事前に設定したカテゴリの中で誰であるかを分類(カテゴリ分け)します。
画像引用元: Scikit-learn Faces recognition example using eigenfaces and SVMs
Example code
ここでは、実際にScikit learnで実装したコード例を載せておきます。内容は、自分で用意したトレーニングデータを元に、SVMに適切な決定境界を学習させるというものです。
実際の実行は他の機械学習Academy同様、こちらのJupyter Notebookをダウンロードしてその中で行ってください。
*Jupyter Notebook使用には、Anacondaがダウンロード済みである必要があります。
Anacondaダウンロード方法は機械学習を用いた画像分類体験をご覧ください。
1. ライブラリのインポートとデータセットの用意
まず、必要なライブラリをインポートします。
|
1 2 3 4 5 6 7 8 |
%matplotlib inline import numpy as np import matplotlib.pyplot as plt from scipy import stats # use seaborn plotting defaults import seaborn as sns; sns.set() |
次に、2クラスにクラス分けされたトレーニングデータセットを用意します。
|
1 2 3 4 |
from sklearn.datasets.samples_generator import make_blobs X, y = make_blobs(n_samples=50, centers=2, random_state=3, cluster_std=0.60) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='brg'); |
※最新版のsklearnを使用する方は上記の1行目を「from sklearn.datasets import make_blobs」としてください
2. クラスによるデータの決定境界
この2つのクラスをうまく分割する直線(決定境界)を引くことを考えます。
|
1 2 3 4 5 6 7 8 9 10 |
xfit = np.linspace(-6.5, 2.5) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='brg') plt.plot([-0.5], [0.8], 'x', color='red', markeredgewidth=2, markersize=10) # draw several dividing lines that perfectly separate the two classes for m, b in [(0.1, 2.3), (-0.6, 1), (-2, -1.4)]: plt.plot(xfit, m * xfit + b, '-k') plt.xlim(-6.5, 2.5) plt.ylim(-2, 6); |
するとこのように、クラス分けをする直線には通常、多数候補が考えられます。 そしてその中でどの直線を選ぶかによって、新しいデータ点をどのクラスと判定するかが変わってきてしまいます。
グラフ上で、赤のバツ印が新しいデータ点だとします。新しいデータのクラスは、そのデータが決定境界より上にあればクラス青、下にあればクラス黄緑と判別されます。つまりどの直線をクラス判別に採用するかによって、このデータのクラスは青と判別されたり黄緑と判別されたりと結果が変わってきてしまうのです。
3. マージンの導入
そこでどの直線をクラス判別に採用するかを決める基準となるのが、マージンと呼ばれる量です。以下で、先ほどの直線のマージンを書き加えたグラフを表示させてみます。
|
1 2 3 4 5 6 7 8 9 10 11 |
xfit = np.linspace(-6.5, 2.5) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='winter') for m, b, d in [(0.1, 2.3, 0.2), (-0.6, 1, 1.8), (-2, -1.4, 4.5)]: yfit = m * xfit + b plt.plot(xfit, yfit, '-k') plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none', color='#AAAAAA', alpha=0.4) plt.xlim(-6.5, 2.5) plt.ylim(-2, 6) |
各直線のまわりのグレーの幅がマージンです。 マージンとはこのように、その決定境界から各クラスの最も近いデータ点への距離となります。 SVMではこのマージンを最大化するような直線が、新しいデータのクラスの判別に最もよいものとして採用されます。これがSVMのアルゴリズムの中身になります。
実際このグラフ上でも、マージンの一番大きい直線が、どのような位置に新しいデータ点が来たとしても、クラスの判別には一番バランスがとれているであろうことが見てとれます。
4. SVMのフィッティングと学習した決定境界の表示
では実際に、このデータセットに対してSVMをフィッティングさせてみます。 その際指定するCパラメータは、採用する決定境界にどれぐらいの誤分類を許すかを表します。 Cパラメータの値は大きければ大きいほど、トレーニングデータの分類に忠実な、”厳しい”決定境界となります。
今回の例のように直線で分割する場合はイメージしづらいですが、曲線などで分割しようとする際は、Cパラメータの値を小さくして、トレーニングデータでの分類に多少の誤りを許した方がよい場合もあります。分割曲線があまり複雑になり過ぎず、新規のデータに対する最終的な判別性能が向上する場合もあるのです。
|
1 2 3 |
from sklearn.svm import SVC # "Support vector classifier" model = SVC(kernel='linear', C=1E10) model.fit(X, y) |
可視化のために、フィッティングをかけたSVMの決定境界を表示する関数を用意します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
def plot_svc_decision_function(model, ax=None, plot_support=True): """Plot the decision function for a 2D SVC""" if ax is None: ax = plt.gca() xlim = ax.get_xlim() ylim = ax.get_ylim() # create grid to evaluate model x = np.linspace(xlim[0], xlim[1], 30) y = np.linspace(ylim[0], ylim[1], 30) Y, X = np.meshgrid(y, x) xy = np.vstack([X.ravel(), Y.ravel()]).T P = model.decision_function(xy).reshape(X.shape) # plot decision boundary and margins ax.contour(X, Y, P, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--']) # plot support vectors if plot_support: ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=300, linewidth=1, facecolors='none'); ax.set_xlim(xlim) ax.set_ylim(ylim) |
それではSVMが学習した決定境界を表示してみます。
|
1 2 |
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='brg') plot_svc_decision_function(model); |
この実線が、SVMが学習した、このデータセットでのマージン(点線までの距離)を最大化する直線(決定境界)ということになります。 このようにして、SVMは学習を行います。
5. 異なるトレーニングデータ数での結果の比較
以下を実行することで、このSVMモデルを異なるトレーニングデータ数でフィッティングしたときの結果をインタラクティブに見ることができます。
最終行のN=[]の中の数字を変えることで、好きなデータ数での結果を見比べることができます。 ぜひいろいろと試してみて、決定境界の変化を追ってみてください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
def plot_svm(N=N, ax=None): X, y = make_blobs(n_samples=200, centers=2, random_state=0, cluster_std=0.60) X = X[:N] y = y[:N] model = SVC(kernel='linear', C=1E10) model.fit(X, y) ax = ax or plt.gca() ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='brg') ax.set_xlim(-1, 4) ax.set_ylim(-1, 6) plot_svc_decision_function(model, ax) from ipywidgets import interact, fixed interact(plot_svm, N=[10, 50, 100, 200], ax=fixed(None)); |
以上がExample codeの内容になります。ぜひJupyter notebook上で動かして見て、理解を深めてください。
まとめ
今回はSupport Vector Machine (SVM) というアルゴリズムについて、コードを動かしながらその仕組みを見てきました。
SVMは特に分類問題によく使われる強力なアルゴリズムです。高速で信頼性も高く、少ないデータでもよい結果が期待できるため、ニューラルネットワークが台頭してきた今も根強い人気があります。今後も覚えておいて損はないアルゴリズムです。
あなたも、Avintonでこのような最先端技術を習得し活用してみませんか?
社員の成長を導きながら、AIやビッグデータなどの最先端技術をプロジェクトに活用していくことが私たちのビジョンです。Avintonの充実した技術研修でスキルアップを図り、あなたのキャリア目標を一緒に達成しませんか?



