このアカデミーでは、機械学習における分類と回帰の違いについて整理します。
この2つの違いを整理することによって、分類のアルゴリズムや回帰のアルゴリズムを学ぶための助けになればと思います。
分類と回帰の位置づけとしては、両方とも教師あり学習にあたります。
機械学習
教師あり学習
・クラス分類
・ニューラルネットワーク(deep Learning)
・回帰分類
教師なし学習
・クラスタリング
・k-means
強化学習
・Q学習
教師あり学習と教師なし学習について解説した記事はこちら
【機械学習入門】教師あり学習と教師なし学習
二ューラルネットワークやQ学習について解説した記事はこちら
【機械学習入門】 深層強化学習の基礎
分類
分類のイメージ
分類の主な目的は、データが属するクラス(Yes,Noのような)を予測することです。
特に、予測するクラス数が2クラスの場合、2値分類と呼ばれます。
具体例としては、ある学生のプロフィールを入力として、その学生が合格か不合格かを予測します。
他の例としては、顧客の購買情報からその顧客が新商品を買うか買わないかを予測します。
これらの予測問題は2値分類に属します。
2クラスより多い分類予測については、多クラス分類として知られています。
具体例としては、学生の課題の詳細な情報から、その学生の評価(S,A,B,etc…)を予測します。
画像に写っている物の判断も多クラス分類問題として知られています。
回帰
回帰の主な目的は、連続値などの値の予測です。
具体例としては、広告予算の増加による商品の売り上げの増加を予測します。
回帰分析には、線形回帰、多項式回帰などが存在します。
図は線形回帰のイメージです。過去の広告予算ごとの売上データをもとに回帰直線を作成します。この回帰直線を利用して、予算から売上を予測します。

線形回帰のイメージ
分類と回帰の違い
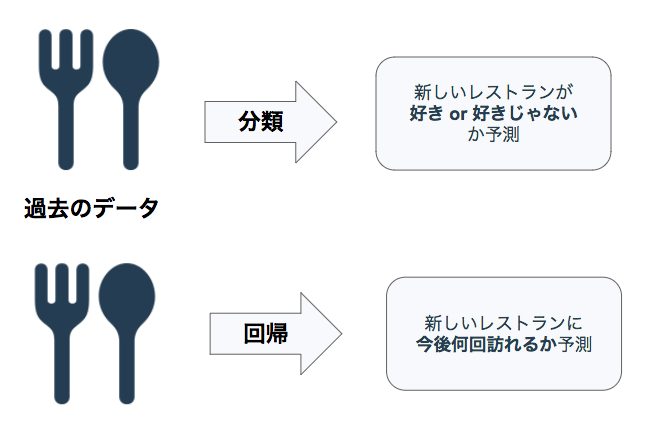
分類と回帰の違いのイメージ
分類の例
過去に訪れた飲食店の情報をもとに、新しい飲食店が気に入るかどうかを予測します。
この予測の目的は、飲食店を気に入る(Yes)か気に入らない(No)かを予測することです。
この問題はクラス分類問題(2値分類)であるといえます。
回帰の例
過去に訪れた飲食店の情報をもとに、新しい飲食店に訪れる回数を予測します。
この予測の目的は飲食店を訪れる回数で、具体的な値を予測します。
回帰分析は過去のデータから何かの値を予測する、教師あり学習に含まれます。
分類と回帰の違いをプログラムを書いて学ぶ
分類と回帰の違いを実際にJupyter Notebook上でプログラムを書きながら学んでみましょう。
こちらからJupyter Notebookをダウンロードしてください。
Jupyter Notebookを使用するにはAnacondaがインストールされている必要があります。
Anacondaのインストール方法は、機械学習を用いた画像分類をご覧ください。
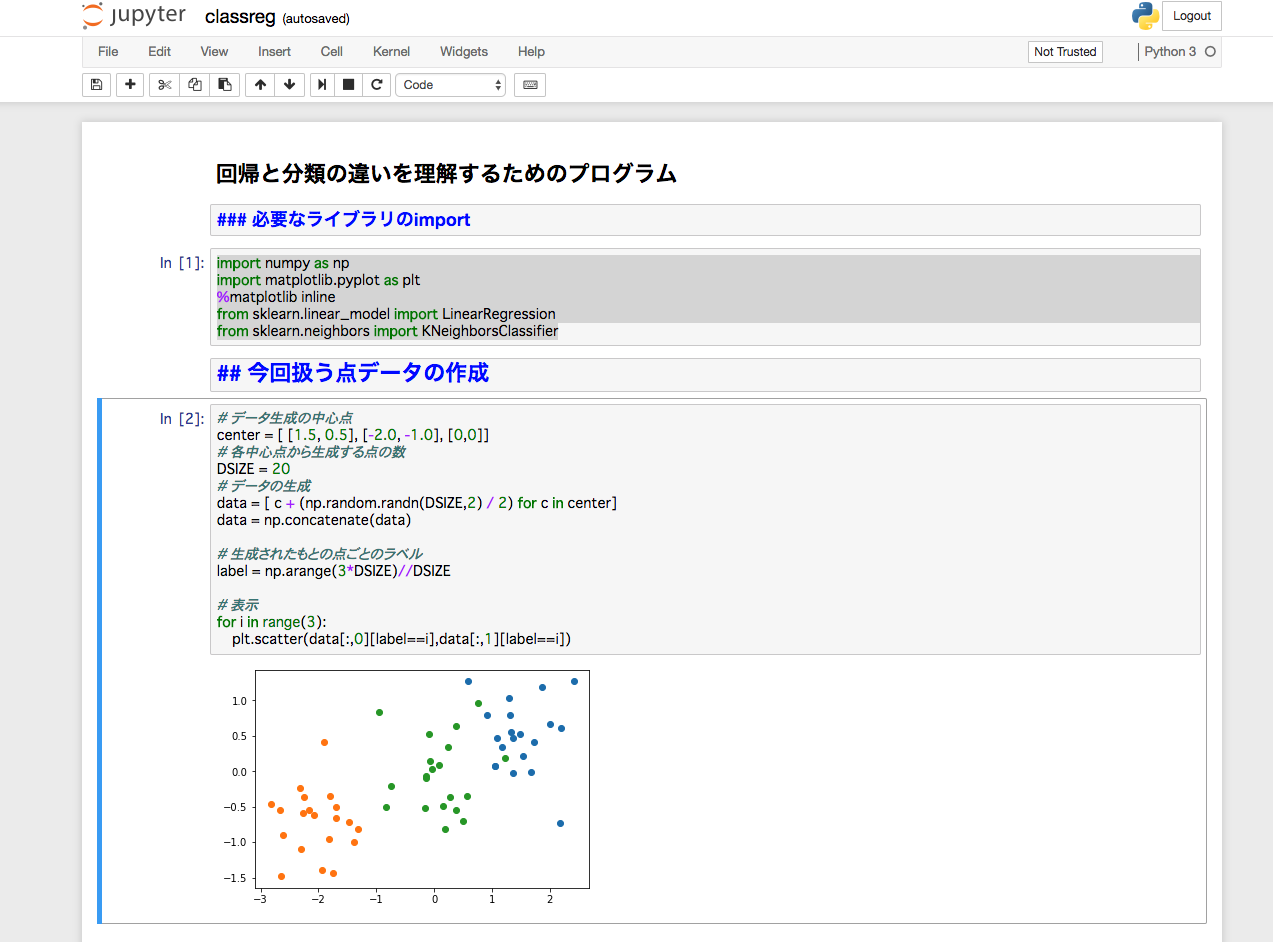
Jupyter Noterbook上でプログラムが実行できます。
以下にJupyter Notebook上にある、コード例を紹介します。
Jupyter Notebookでは、コードを書くと結果がすぐに表示され、プログラミングを書きながら学ぶことができます。
必要なライブラリのインポート
|
1 2 3 4 5 6 |
import numpy as np import matplotlib.pyplot as plt %matplotlib inline from sklearn.linear_model import LinearRegression from sklearn.neighbors import KNeighborsClassifier |
今回扱う点データの作成
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# データ生成の中心点 center = [ [1.5, 0.5], [-2.0, -1.0], [0,0]] # 各中心点から生成する点の数 DSIZE = 20 # データの生成 data = [ c + (np.random.randn(DSIZE,2) / 2) for c in center] data = np.concatenate(data) # 生成されたもとの点ごとのラベル label = np.arange(3*DSIZE)//DSIZE # 表示 for i in range(3): plt.scatter(data[:,0][label==i],data[:,1][label==i]) |
線形回帰の例
今回の線形回帰では、先ほど生成した点のx座標を入力として、y座標を予測するモデルを作成する
データの分離
点データをx座標(予測モデルに入力する値)と、y座標(予測したい値)に分ける
|
1 |
X, y = np.split(data, 2, axis=1) |
線形回帰の予測モデルを作成し、適当なx座標を入力して、y座標の値を予測する
|
1 2 3 4 |
lr = LinearRegression().fit(X, y) test_X = np.arange(-4, 5) test_X = test_X.reshape(len(test_X), 1) y_predict = lr.predict(test_X) |
予測結果の確認
|
1 |
print(y_predict) |
[[-1.25995015]
[-0.95403541]
[-0.64812067]
[-0.34220593]
[-0.03629118]
[ 0.26962356]
[ 0.5755383 ]
[ 0.88145304]
[ 1.18736778]]
|
1 2 3 4 5 6 7 |
plt.scatter(X, y, label="data") plt.plot(test_X, y_predict, label='linear model') plt.xlim(-4,4) plt.ylim(-4,4) plt.title("Predict result") plt.grid() plt.legend() |
今回の予測モデルの式
y=x∗a+b
|
1 2 |
y_predict_function = lambda x: x * lr.coef_ + lr.intercept_ print(y_predict_function(3)) |
分類の例
今回の分類では、点のx,y座標を入力として、その点が属するクラス(label)を予測するモデルを作成する。
K-Nearest Neighbor(KNN)の予測モデルを作成
data(x, y座標)とそれに対応するlabel(点が属するクラスを表す)のペアを入力として、
KNNの予測モデルを生成する。
|
1 |
neigh = KNeighborsClassifier().fit(data, label) |
適当な点のx, y座標を入力して、その点が属するクラスを予測する
|
1 2 |
test_Xy = np.array([np.random.rand(10) * 6 - 3, np.random.rand(10) * 4 - 2]).T predict_label = neigh.predict(test_Xy) |
予測結果の確認
|
1 |
print(predict_label) |
[0 0 2 1 2 2 0 1 2 0]
分類結果の描画
★がtest_Xyの点で、それぞれの色がクラスに対応している
(test_Xyの座標によって、★の色が黄色とか紫に変わることがある…)
|
1 2 3 4 5 |
for i in range(3): rgb = [False for i in range(3)] rgb[i] = True plt.scatter(data[:,0][label==i],data[:,1][label==i], c=rgb) plt.scatter(test_Xy[:,0][predict_label==i], test_Xy[:,1][predict_label==i],c=rgb, marker="*", s=200) |
まとめ
クラス分類と回帰は、データと対応する正解をもとに予測をする教師あり学習となります。
対象のデータが属するクラスを予測するときは分類、値を予測するときは回帰となります。
あなたも、Avintonでこのような最先端技術を習得し活用してみませんか?
社員の成長を導きながら、AIやビッグデータなどの最先端技術をプロジェクトに活用していくことが私たちのビジョンです。Avintonの充実した技術研修でスキルアップを図り、あなたのキャリア目標を一緒に達成しませんか?



